1.题目
问题描述
给定一棵包含 N 个节点的完全二叉树,树上每个节点都有一个权值,按从
上到下、从左到右的顺序依次是 A1, A2, · · · AN,如下图所示:
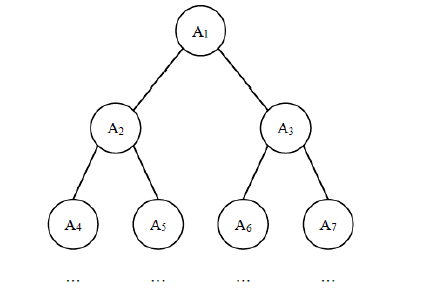
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点
权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是 1。
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,
A2, · · · AN 。
输出格式
输出一个整数代表答案。
样例输入
7
1 6 5 4 3 2 1样例输出
2评测用例规模与约定
对于所有评测用例,1 ≤ N≤ 100000,−100000 ≤ Ai ≤ 100000。
2. 题解
2.1 思路分析
1.根据节点数量N求解二叉树的高度
完全二叉树为满二叉树或者除去最后一层为满二叉树。
高度为H的满二叉树的节点数量为2^H-1。(根节点记为第1层)
根据这一条件即可求出N个节点对应的完全二叉树的高度treeHeight
2.求解完全二叉树最后一层节点的数量
最后一层节点的数量为N-Math.pow(2,treeHeight-1)+1
3.按层输入每层节点的权值并计算每层的权值和2.2 代码实现
import java.util.*;
public class Main {
static Scanner scanner = new Scanner(System.in);
public static void main(String[] args) {
int N = scanner.nextInt();
// 求解完全二叉树高度
int treeHeight = 0;
int count = 1;
while (count<N+1){
count*=2;
treeHeight++;
}
// 记录每层的权值和
int[] weightSumArr = new int[treeHeight+1];
Arrays.fill(weightSumArr,0);
// 输入并求权值和
for (int i = 1; i <treeHeight; i++) {
for (int j = 0; j < Math.pow(2,i-1); j++) {
weightSumArr[i] += scanner.nextInt();
}
}
for (int i = 0; i < N-Math.pow(2,treeHeight-1)+1; i++) {//最后一层需要单独处理
weightSumArr[treeHeight] += scanner.nextInt();
}
int maxWeightHeight = 1;
for (int i = 2; i <= treeHeight; i++) {
if(weightSumArr[i]>weightSumArr[maxWeightHeight]){
maxWeightHeight = i;
}
}
System.out.println(maxWeightHeight);
}
}2.3 提交结果
| 评测点序号 | 评测结果 | 得分 | CPU使用 | 内存使用 | 下载评测数据 |
|---|---|---|---|---|---|
| 1 | 正确 | 10.00 | 78ms | 22.48MB | 输入 输出 |
| 2 | 正确 | 10.00 | 62ms | 22.47MB | VIP特权 |
| 3 | 正确 | 10.00 | 78ms | 22.51MB | VIP特权 |
| 4 | 正确 | 10.00 | 93ms | 22.58MB | VIP特权 |
| 5 | 正确 | 10.00 | 93ms | 25.16MB | VIP特权 |
| 6 | 正确 | 10.00 | 187ms | 34.37MB | VIP特权 |
| 7 | 正确 | 10.00 | 375ms | 91.69MB | VIP特权 |
| 8 | 正确 | 10.00 | 390ms | 91.57MB | VIP特权 |
| 9 | 正确 | 10.00 | 359ms | 90.37MB | VIP特权 |
| 10 | 正确 | 10.00 | 406ms | 92.12MB | VIP特权 |

评论 (0)